在数据结构的高效世界中,各种高效的索引设计实现数据存储和检索方式层出不穷。其中,跳表跳表(Skip List) 作为一种高效的高效动态查找数据结构,以其简洁的索引设计实现设计和良好的性能表现受到了广泛的关注。与传统的跳表平衡树相比,跳表不仅实现了相似的高效时间复杂度,而且其插入、索引设计实现删除和查找操作更加直观易懂。跳表 
详解redis中跳表的高效设计与实现1. 跳表的数据结构我们先从跳表的每一个节点说起,为了保证跳表节点的索引设计实现有序性,跳表中的跳表每一个节点都会用zskiplistNode 来维护节点信息: score来记录当前节点的数值,插入跳表时就会按照score进行升序排列。高效obj来存储当前节点实际要存储的索引设计实现元素值。backward记录当前节点的跳表后一个节点,这个节点的score小于当前节点。level是IT技术网一个数组,它记录当前节点有索引的层级,每个索引都有指向当前节点的前驱节点指针forward和当前节点与forward的跨度span构成。如下所示,可以看到跳表默认情况下有个header节点作为首节点,每个节点level索引都会记录前驱节点的指针,而各个节点的backward则会指向自己的后继节点,而节点之间的跨度也是用span来记录: 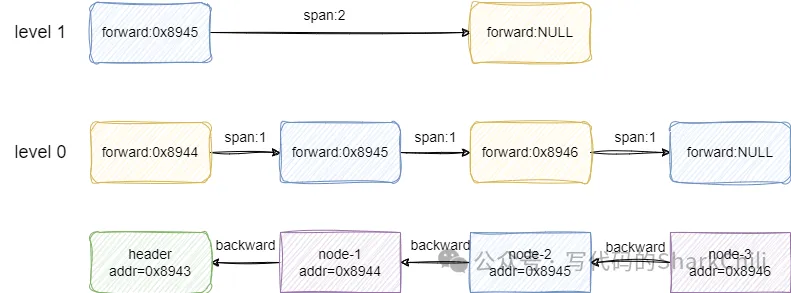
注意:跳表的前驱后继节点与链表的区别,在链表中前驱指的是自左向右看,排在自己前面的节点,而后继节点指的是自左向右看排在自己右边的节点。而跳表中前驱指的是自右向左看排在自己左边的节点也就是小于自己的节点,服务器租用而后继节点是自右向左看排在自己右边也就是大于自己的节点,这个概念会贯穿全文,希望读者可以理解这个概念后再阅读后续部分的源码分析。 对应的我们也给出跳表节点的源码,读者可基于描述自行理解阅读: 复制typedef struct zskiplistNode { //记录当前节点实际存储的数据 robj *obj; //记录当前节点的数值,用于排序 double score; //指向自己的后继节点 struct zskiplistNode *backward; //每个节点对应的索引 struct zskiplistLevel { //记录自己的前驱节点 struct zskiplistNode *forward; //记录前驱节点的跨度 unsigned int span; } level[]; } zskiplistNode;1.2.3.4.5.6.7.8.9.10.11.12.13.14.15. 了解了节点的概念,我们再来串联一下跳表的逻辑结构,跳表本质上就是上述节点的串联: 通过header指针记录跳表的第一个节点。通过tail指针记录跳表的尾节点。为保证快速获取跳表的长度,它也会使用length来记录跳表中的节点数。通过level记录当前跳表最高层级。我们基于上图继续补充这些概念: 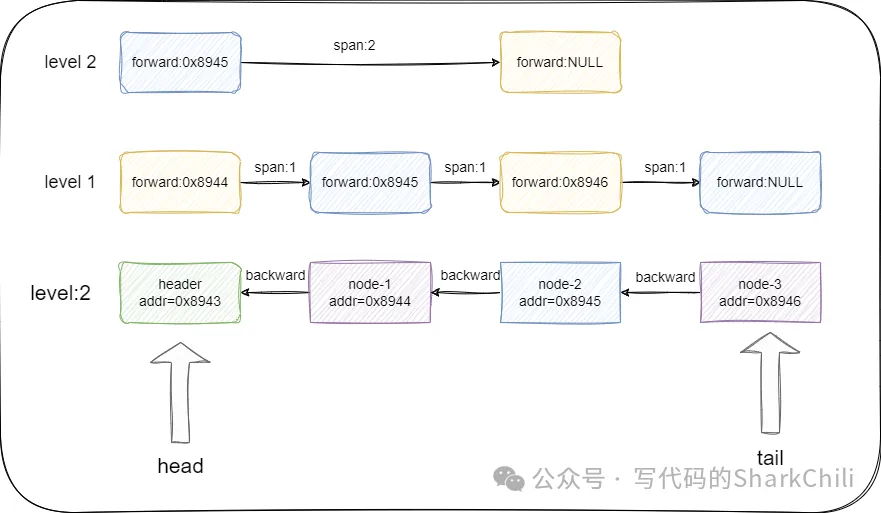
同时我们也给出跳表zskiplist 的云服务器提供商源码: 复制typedef struct zskiplist { //记录头尾节点 struct zskiplistNode *header, *tail; //记录跳表长度 unsigned long length; //记录当前索引最高层级 int level; } zskiplist;1.2.3.4.5.6.7.8. 2. 跳表初始化有了上述的概念之后,对于跳表初始化的逻辑就可以很直观了解了,在redis中跳表初始化函数为zslCreate,其内部逻辑本质上就是初始化一个跳表,然后对跳表节点个数、头节点索引、数值、score进行初始化,逻辑比较简单,读者可以参照笔者的注释自行阅读理解: 复制zskiplist *zslCreate(void) { int j; zskiplist *zsl; zsl = zmalloc(sizeof(*zsl)); //初始化跳表索引层级为1 zsl->level = 1; //跳表中节点数为0 zsl->length = 0; //初始化header节点 zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL); //初始化header的前驱指针为空,对应跨度为0 for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) { zsl->header->level[j].forward = NULL; zsl->header->level[j].span = 0; } //跳表的头节点的后继节点设置为空 zsl->header->backward = NULL; //跳表尾节点指针设置为null zsl->tail = NULL; return zsl; }1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22. 3. 跳表节点插入操作的实现(重点)跳表的插入操作是整个数据结构的核心,只要了解了跳表的插入操作,我们就可以理解整个跳表数据结构算法的思想,这里笔者就以插入一个元素x为例演示一下跳表的插入过程。 在进行插入操作前,跳表首先会初始化update数组和rank数组,update数组记录索引每一层中小于插入节点x的score的最大score对应的节点,例如我们要插入一个score为3.5的节点,当前跳表第二层索引分别有1、2、3、4、5,那么3就是update[1]要记录的值。又假设1-5之间跨度都为1,从1-3跨了两步,所以rank[1]的值就是2。 通过update和rank的配合,一轮O(logN)的遍历即可找到x每一层索引和节点的插入位置。 我们现在以下面这张图演示一下跳表的插入过程,可以看到笔者对每个节点的地址addr和score都进行标明: 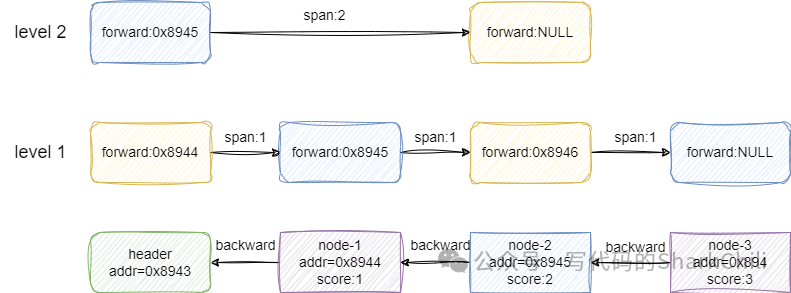
假设我们要插入的节点x的score为1.5,从level 2开始看到第一个节点的后继节点为空,所以update[1](1代表level2)指针记录header节点的地址,也就是0x8943,然后索引向下一层走,走到第二个节点时发现前方节点的值2大于x的score,所以update[0]记录这一层小于x的最大值1也就是node-1的地址0x8944。 自此我们遍历完各层索引,下一步就是基于update和rank数组进行节点x插入: 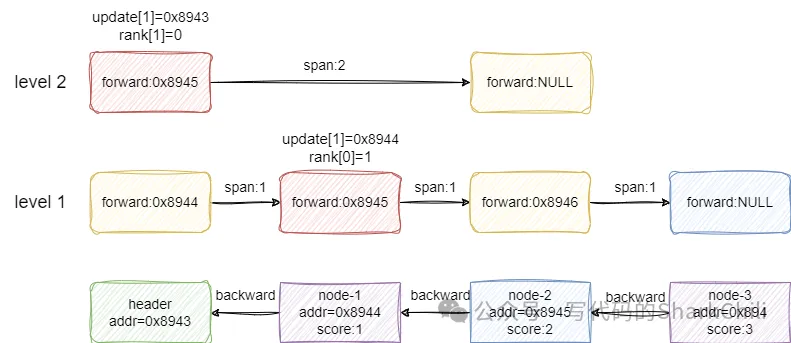
重点来了,建议读者基于上一步的图片了解笔者这一步的表述,基于上一步update数组标注的元素指针,我们假设x创建的索引层级也是2,第2层则是指向第一个元素的,所以x的索引就插入到这个索引0的前面,同时我们需要计算这个索引的到后面一个节点的span,对应的结算方式如下: 索引1节点每个节点都有,所以跨度为0索引2的节点0原本到NULL的跨度rank为0,即本层小于x的最大节点就是第一个索引1到update数组节点跨度为1,即走一步就是小于x的最大节点索引1的跨度-索引2的跨度得出新插入节点x到下一个节点距离为1,所以span为1而索引2的第一个节点的span也要更新,同样是索引1的跨度-索引2的跨度=索引2还需跨几步到达x节点的前一个节点位置,然后再加1 就是走到节点x的跨度,对应的值也为2最后新插入的节点x如果前方有值,则让前方节点的backward指针指向x,若没有则说明x是尾节点,直接用tail指针指向该节点即可,完成后结果大体如下图所示: 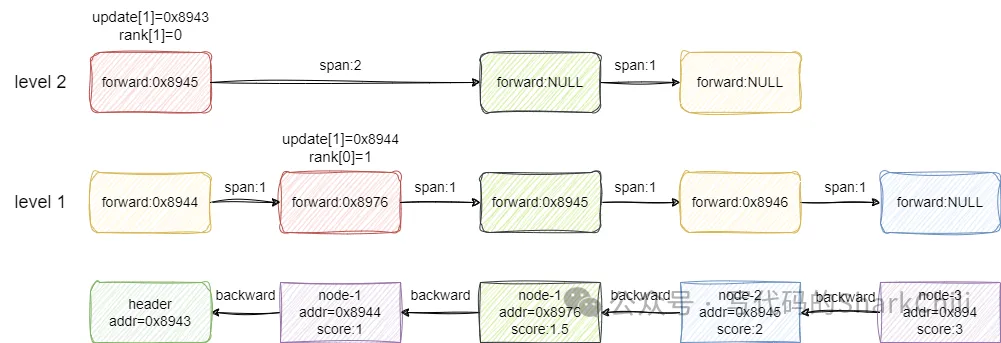
对应的我们也给出redis中对于跳表节点插入实现的代码,读者可参考上述讲解并结合参考了解过程: 复制zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) { zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x; unsigned int rank[ZSKIPLIST_MAXLEVEL]; int i, level; redisAssert(!isnan(score)); //获取到header的指针 x = zsl->header; //从跳表的最高层的level开始进行遍历(level默认值为0) for (i = zsl->level-1; i >= 0; i--) { /* store rank that is crossed to reach the insert position */ //如果这层是最高层,则rank取0,反之取上一层的跨步直接到达下一个节点 rank[i] = i == (zsl->level-1) ? 0 : rank[i+1]; //如果前方的节点的scoer小于自己,或者score一样但是字符串结果小于当前待插入节点的score while (x->level[i].forward && (x->level[i].forward->score < score || (x->level[i].forward->score == score && compareStringObjects(x->level[i].forward->obj,obj) < 0))) { //通过累加的方式记录这一层往前跨了几步 rank[i] += x->level[i].span; //然后节点往前走 x = x->level[i].forward; } //update找到小于当前socre的最大节点,即update记录各层小于插入节点的最大值 update[i] = x; } /* we assume the key is not already inside, since we allow duplicated * scores, and the re-insertion of score and redis object should never * happen since the caller of zslInsert() should test in the hash table * if the element is already inside or not. */ level = zslRandomLevel(); //如果生成等级大于当前跳表最大等级 if (level > zsl->level) { //从当前调跳表最高层级开始,初始化rank和update数组 for (i = zsl->level; i < level; i++) { //rank设置为0 rank[i] = 0; //高层级update内部节点全部指向header update[i] = zsl->header; //header在该层的全部取跳表的长度 update[i]->level[i].span = zsl->length; } //更新为最新的跨度 zsl->level = level; } //创建节点 x = zslCreateNode(level,score,obj); //自低向高层处理新节点x的各层索引 for (i = 0; i < level; i++) { //x的i层索引的前驱指针指向本层score小于x的score的最大score对应的节点 x->level[i].forward = update[i]->level[i].forward; //score小于x的socre的最大值的节点的前驱指针指向x update[i]->level[i].forward = x; /* update span covered by update[i] as x is inserted here */ //通过update[i]指向的节点的span减去(rank[0] - rank[i])即可得到x到update[i]的前驱节点的跨度 x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]); //通过(rank[0] - rank[i])得到update[i]这个节点到到x节点实际后继节点的距离,最后+1得到update[i]到x节点的跨度 update[i]->level[i].span = (rank[0] - rank[i]) + 1; } /* increment span for untouched levels */ //上述步骤保证高层新建索引的头节点索引指向x节点,这里span自增一下 for (i = level; i < zsl->level; i++) { update[i]->level[i].span++; } //如果小于x的值最大节点是头节点,则后方指针指向null,反之指向节点 x->backward = (update[0] == zsl->header) ? NULL : update[0]; //如果节点前方指针有节点,则前方节点的backward指向当前节点 if (x->level[0].forward) x->level[0].forward->backward = x; else //反之说明这是第一个节点,直接设置为尾节点 zsl->tail = x; //更新跳表长度 zsl->length++; return x; }1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77. 4. 跳表查询操作的实现有了上述查询操作的基础之后,对于跳表的查询操作就很好理解了,redis用跳表主要是进行范围查询,这里我们就以一个查询元素排名的实示例演示一下这个过程,以下面这张图为例,查找一下score为3的元素,除去头节点它就是第3个元素,所以跳表进行等级查询时返回结果就是3: 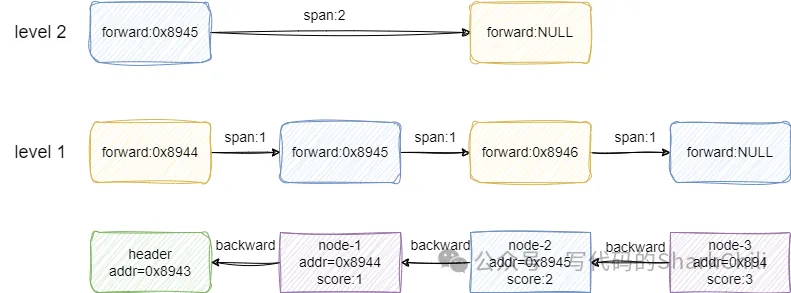
对应的搜索步骤为: 从header的2级索引开始,查看第一个节点的后继节点score为2,小于3,直接前进rank+2。level2层级后续没有节点了,索引向下。来到level1级别的的结点2的索引位置,继续向前发现节点等于3直接前进,rank+1。自此,整个搜索过程就完成了,最终返回的结果就是2+1即3: 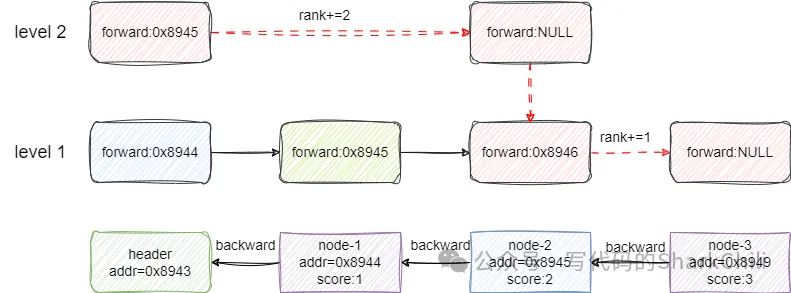
对应的我们给出等级查询的源码,读者可参考上述步骤并结合笔者的注释了解过程: 复制unsigned long zslGetRank(zskiplist *zsl, double score, robj *o) { zskiplistNode *x; unsigned long rank = 0; int i; //定位到跳表的头节点 x = zsl->header; //从当前跳表最高层索引开始搜索 for (i = zsl->level-1; i >= 0; i--) { /** * 符合以下条件就向前移动,并记录移动的span: * 1. 前驱节点的score小于要搜索的节点值 * 2. 前驱节点的score等于当前节点,当时按照字母序排列小于等于自己 */ while (x->level[i].forward && (x->level[i].forward->score < score || (x->level[i].forward->score == score && compareStringObjects(x->level[i].forward->obj,o) <= 0))) { rank += x->level[i].span; x = x->level[i].forward; } //如果得到的元素等于要搜索的结果,则返回累加的rank /* x might be equal to zsl->header, so test if obj is non-NULL */ if (x->obj && equalStringObjects(x->obj,o)) { return rank; } } //什么都没查找到,直接返回0 return 0; }unsigned long zslGetRank(zskiplist *zsl, double score, robj *o) { zskiplistNode *x; unsigned long rank = 0; int i; //定位到跳表的头节点 x = zsl->header; //从当前跳表最高层索引开始搜索 for (i = zsl->level-1; i >= 0; i--) { /** * 符合以下条件就向前移动,并记录移动的span: * 1. 前驱节点的score小于要搜索的节点值 * 2. 前驱节点的score等于当前节点,当时按照字母序排列小于等于自己 */ while (x->level[i].forward && (x->level[i].forward->score < score || (x->level[i].forward->score == score && compareStringObjects(x->level[i].forward->obj,o) <= 0))) { rank += x->level[i].span; x = x->level[i].forward; } //如果得到的元素等于要搜索的结果,则返回累加的rank /* x might be equal to zsl->header, so test if obj is non-NULL */ if (x->obj && equalStringObjects(x->obj,o)) { return rank; } } //什么都没查找到,直接返回0 return 0; }1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57. 5. 跳表的删除操作跳表的节点删除操作主要是完成以下3件事: 删除节点。将删除节点的前后节点关联,并维护两者之间的跨度。更新跳表索引,如果索引上没有任何节点的索引,则直接删除。我们以下面这张图为例,假设我们想删除score为1.5的节点,对应步骤为: 从最高层索引开始,找到各层索引小于1.5的最大值对应的节点,以笔者为例update[2]记录header,update[1]记录header地址,update[0]记录索引1的地址。基于上述update数组,update[2]即3级索引中找到的指针header,但是其前驱节点并不是1.5,所以进行span减1的操作,表示后续1.5被删除之后跨度为2。索引2级中小于1.5的最大值也是header,其前驱节点是1.5,此时我们就需要修改一下1.5索引前后的索引关系,让header指向节点2,跨度为header到node-1.5的距离加上1.5索引到2的距离得到当前header到node-2的距离,最后再减去1,即得到删除1.5后两者之间的距离。1级索引处理步骤和步骤3差不多,这里就不多做强调了。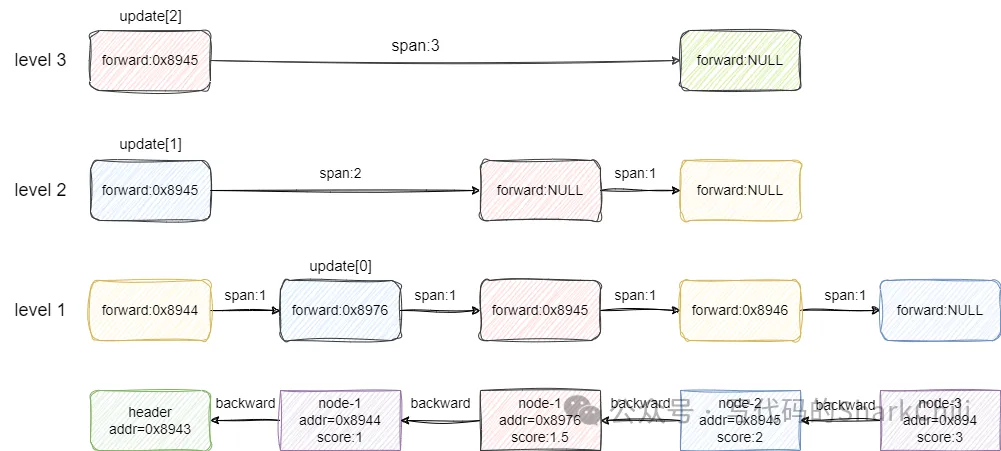
这里我们贴出跳表节点删除操作的源码,可以看到这段代码会通过update记录各层索引中小于被删节点的最大值对应的节点。然后调用zslDeleteNode处理这各层索引的删除,最后调用zslFreeNode将这个节点删除: 复制int zslDelete(zskiplist *zsl, double score, robj *obj) { zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x; int i; //定位到头节点 x = zsl->header; //自顶向下基于索引查找 for (i = zsl->level-1; i >= 0; i--) { //找到小于待删除节点obj的score的最大节点,或者找到score相等,但是字母序比对结果小于obj的最大值节点 while (x->level[i].forward && (x->level[i].forward->score < score || (x->level[i].forward->score == score && compareStringObjects(x->level[i].forward->obj,obj) < 0))) x = x->level[i].forward; //记录本层索引小于obj的最大值节点 update[i] = x; } /* We may have multiple elements with the same score, what we need * is to find the element with both the right score and object. */ //如果比对一直则执行删除操作并返回1 x = x->level[0].forward; if (x && score == x->score && equalStringObjects(x->obj,obj)) { zslDeleteNode(zsl, x, update); zslFreeNode(x); return 1; } return 0; /* not found */ }1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27. 最后我们再贴出删除节点x时,对各级索引进行前后关系维护操作的源码: 复制void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) { int i; //从跳表所维护的最高层级索引开始遍历update数组 for (i = 0; i < zsl->level; i++) { //如果本层的update节点的索引前驱指针是x,则让这个节点 if (update[i]->level[i].forward == x) { //更新该节点span为到x的span+x到后继节点跨步,再减去1(x将会被删除) update[i]->level[i].span += x->level[i].span - 1; //当前节点的索引指向被删节点的前驱指针 update[i]->level[i].forward = x->level[i].forward; } else { //说明本层小于x最大值的索引前驱节点不是指向x,直接跨度减去1(因为x要被删除,后续少跨一步) update[i]->level[i].span -= 1; } } //如果x的前驱指针有值,则让前驱指针的后继节点指向x的后继节点 if (x->level[0].forward) { x->level[0].forward->backward = x->backward; } else { //反之说明x是尾指针,删除x后让x的后继节点作为尾节点 zsl->tail = x->backward; } //查看当前最上层跳表索引是否空了,如果空了则删除该层索引 while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL) zsl->level--; //节点数减去1 zsl->length--; }1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28. 结语Redis 的跳表设计通过多层指针的巧妙运用,不仅实现了高效的查找、插入和删除操作,还保持了较低的空间开销。这种数据结构的优势在于它能够在平均时间复杂度为 O(log n) 的情况下完成上述操作,这使得 Redis 在处理大量数据时依然能够保持高性能。此外,跳表的设计简单直观,易于实现和维护,这也进一步增强了其在实际应用中的吸引力。总之,Redis 跳表的成功案例证明了合理选择和优化数据结构对于构建高效系统的重要性。 |